Algebra Review - Rational Expressions
1. Simplifying Rational Expressions
A rational expression is basically a fraction. Here is a property of rational expressions that you should know:
![]()
Now we shall apply it to several examples:
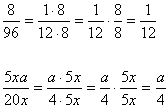
Now we move onto exponents and powers. Remember the following rule:
![]()
Remember that if you have a negative exponent, such as x-2, it is similar to x-2/1 and can be changed to 1/x2. Now some more examples:
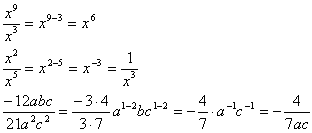
Removing Common Factors
Now another type of simplification - where you remove a common factor. The following examples should be enough for you to understand. Just remember the basic (x + y)2 rules and the other ones, and apply them to the problems, and you should be able to figure it out.
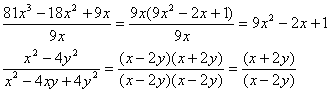
2. Multiplying and Dividing Rational Expressions
When you multiply, you do it the same as you multiply fractions. Just simplify at the end and you're done. Take a look at the following rules and examples and you should do fine.
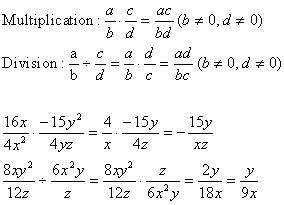
3. Adding and Subtracting Rational Expressions
This is very similar to adding and subtracting fractions. You must make sure the denominators are the same before you are able to add or subtract. Look at the rules and then the examples.
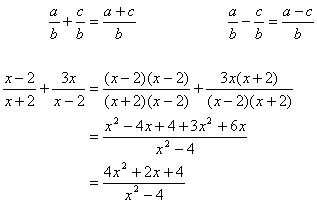
4. Solving Rational Expressions
All you have to do is do whatever you must to solve for the unknown. That means combining terms, combining fractions, cross-multiplying, etc. Here is one basic example:
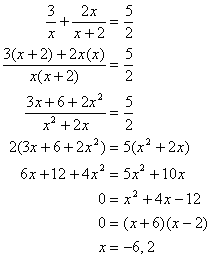
Be sure to check your solutions to see if they are reasonable, such as making sure the denominator is not zero, or if the answer works out.
5. Rate Problems
On hold - until a visitor requests that I work on this section.