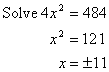
Algebra Review - The Quadratic Equation and Factoring
1. Solving Equations Like 4x2 + 20 = 320
It is useful to know square roots in order to make the process easier. However, if you are allowed to use a calculator, then it is much easier.
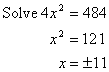
2. Factoring Equations to Solve
If you have to solve something like: 4x2 - 400x = 0, it is easier to factor.
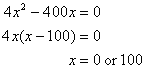It is equal to zero when either the 4x or (x - 100) is zero.
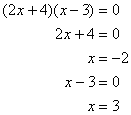
Removing Common Factors
If you have a long expression such as 3x3 + 6x2 - 12x, you can simplify it by factoring out common factors that exist in every term. Here we can see that an x and a 3 occurs in every term. So factoring results in:
3x(x2 + 2x - 4)
Another example: 14a4 + 21a3 - 7a2 = 7a2(2a2 + 3a - 1)
If you need to solve something such as 28x2 + 7x = 0, factor and set each part equal to zero.
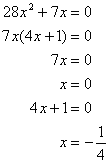
3. Factoring Difference of Two Squares
Remember this rule:
?
Well now, instead of going from A to B, you will go from B to A.
 |
Just break it
down into two parts. Take the first term and take the positive square root,
and then you can turn them into (x + y)(x -y) easily. |
4. Factoring Perfect Squares
Now you will factor more complex squares that look similar to:
 |
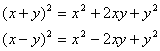
Look at the last term and take the square root of it. Then the middle number and divide it by the square root. If it becomes 2, then you have your numbers. The sign on the middle term determines the sign in the final reduced term. Look and interpret the examples. |
5. Factoring Trinomials
This will only work if you practice and learn to recognize unconsciously the correct numbers. Just look at the examples.
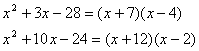
If you were solving each equation, set each section in parenthesis equal to zero. For example, (x + 7) = 0 and (x - 4) = 0 and your resulting answers are x = -7 and 4.
For more complex trinomials such as 3x2 + 5x - 2, you will have to try each one. You know the form will be:
(3x ± ?)(x ± ?)
You just keep trying the numbers until it comes out.
6. Quadratic Equation
is the most important equation you will learn. It allows you to solve equations
that are unfactorable. Since you probably have learned this in class, I will not
bother conjuring up examples. Just remember the equation and apply it. You
should have two resulting answers.