Algebra Review - Square Roots

1. The Pythagorean Theorem

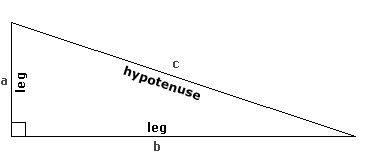
This is very important to remember. The Pythagorean theorem applies to right triangles.

Sides a and b are called the legs. The longest side is always called the hypotenuse.

The basic relationship between the sides that you must know and remember is this equation:

            a2 + b2 = c2

If a = 3, b = 4, c = ?

Use the equation to solve it out:
        32 + 42 = c2
        9 + 16  =
            25    = c2
                5 = c

2. Square Roots

A square root symbol is: .

If you have a number, such as 5, and you square it, as in multiply it by itself, or 5 x 5, you get 25. 25 is the square of 5. If you take the square root of 25, or , you will get 5 or -5. Why are there two answers? If you multiply 5 x 5, you will get 25. If you multiply 5 x -5, you will also get 25.

Some examples:

Take . If x < 0, then there is no square root. If x = 0, then there is only one square root. If x > 0, then there are two possible square roots: .

Notice that when you square a number less than one, it is less than the original number.

If you square one, you get one.

If you square a number greater than one, the answer is greater than the original number.
  Some Rules:

If x < 1, then x < x2 and > x.
If x = 1, then x = x2 and = x.
If x > 1, then x < x2 and < x.

Multiplying and Dividing Square Roots

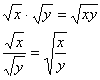
The first rule is the basic multiplication rule.
The second is to help with simplifying division of square roots.

Simplifying Square Roots

If you have a number such as , you can simplify it.

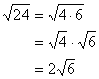
Adding and Subtracting Square Roots

When you add or subtract square roots, you must make it so the number under the square root matches. Otherwise you cannot add or subtract.

Here we made it so all the square roots were the square root of 3.

3. Integers, Rational, Irrational, and Real Numbers

Integers are whole numbers, such as -1, 0, 1, 2, and so on.

Rational numbers can be written as a ratio of numbers, such as 1/2, 3/2, -5/10, and so on. All integers are rational numbers because 5 can be written as 5/1.
Numbers such as 1/3 = 0.3333.... are rational because their decimals repeat. Any decimal number that has repeating digits are rational.

Irrational Numbers are numbers that never end or never repeat.

Real numbers include all rational and irrational numbers.

4. Indirect Measurement

Basically use the Pythagorean theorem to solve for the third distance. If you know two of the measurements, you can always find the third by using the rule: a2 + b2 = c2.

< Back to Algebra Review